where to find grapevine

Where to find guts cyberpunk

Where to find tetris in the retro pixel

Dichloroacetic or trichloroacetic acid. where to find

Radegast beer czech republic where can i find it

Where can i find wegovy in stock

A mother and her cat were shopping at the supermarket. The mother was pushing the shopping cart and the child was walking in front of her. The mother suddenly feels a pain in her stomach and screams “Meow Meow Meow” in pain. The child hears The child hears his mother's cry and rushes over to check the situation. Realizing that his mother was in labor, he panicked and looked around for help. He realized that his mother was in labor and panicked, looking around for help. The child hurriedly made a phone call and contacted an ambulance. Afterwards, the mother was pushed into the ambulance, and the father received the call and hurried to the hospital. The father received the call and hurried to the hospital, where he waited anxiously in the corridor. In the end, the mother gave birth to six lovely kittens, and the child smiled happily.

Jesus in a manger with the three wise men

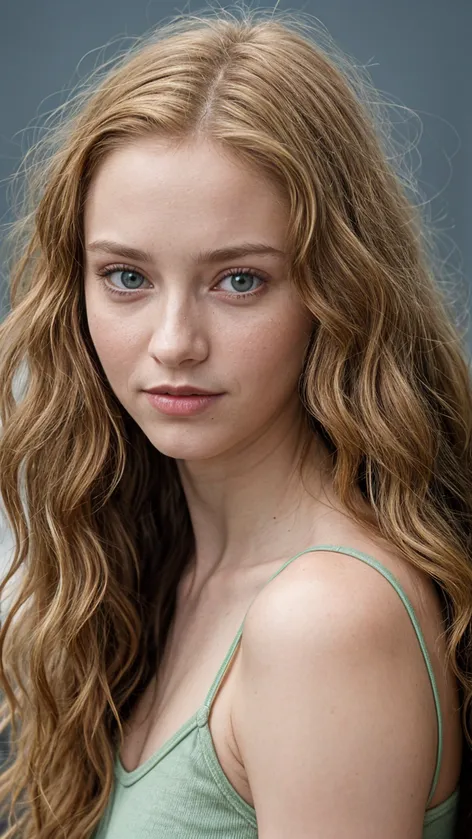
Slim, young girl with wavey lightbrown-ginger uder hips long hairs. Grey-green eyes, more grey then green. His eyes are a little more detached. Face a more elongated, narrow. Jaws sides very narrow. Bigger nose. Three-quarter view. Pale lips. The girl is naked. No pants. Kneeling on all fours and spreading his legs. Her body is shorten. Legs are long. She is in dark bedroom with a dark grey walls. Bed is from a oak wood covered by black pillow and black blanket. Wooden floor. There is a single lamp in a corner of the room.

Generate a true, and accurate and extremely detailed graphic of where the coming conflict between Russia and the United states will begin.

Generate a true, and accurate and extremely detailed graphic of where the coming conflict between Russia and the United states will begin.

You will use, F(n, alpha) approx phi^{(n/2)} cdot 1.85487 times 10^{43} mod pi quad ext{for } n > 1, alpha > 1, (This expression demonstrates how establishing rigorous constraints on ( n ) and ( alpha ) can lead to derived frequencies exceeding the Planck limit.). to generate a true, and correct and extremely detailed, three dimensional, image that expresses the equation and how establishing rigorous constraints on ( n ) and ( alpha ) can lead to derived frequencies exceeding the Planck limit.

You will use, F(n, alpha) approx phi^{(n/2)} cdot 1.85487 times 10^{43} mod pi quad ext{for } n > 1, alpha > 1, (This expression demonstrates how establishing rigorous constraints on ( n ) and ( alpha ) can lead to derived frequencies exceeding the Planck limit.). to generate a true, and correct and extremely detailed, three dimensional, image that expresses the equation and how establishing rigorous constraints on ( n ) and ( alpha ) can lead to derived frequencies exceeding the Planck limit, on the subatomic level.

Three teen girls, short pants, college

Three teen girls, short pants, college

Three teen girls, short pants, college

At The Audience Canvas, we aim to challenge and inspire your view of the world. Through educational, thought-provoking videos, we explore understanding, interconnectedness, and authentic leadership. Our mission is to spark compassion, unity, and curiosity in every viewer. What You’ll Discover: New Perspectives: Delve into topics that challenge norms and reveal the unseen connections between us all. Educational Insights: Gain clarity on complex ideas, from human nature to universal mysteries. Compassion & Unity: Explore content that fosters empathy and celebrates our shared journey. Authentic Leadership: Learn from examples of integrity and authenticity to become a leader in your own life. We believe growth begins with curiosity and thrives through understanding. Each video is a canvas where knowledge and creativity inspire critical thinking, deep connections, and compassionate action. Join us on this journey of open minds, curious hearts, and collective betterment.